, процесс без последействия, - случайный процесс, эволюция к-рого после любого заданного значения временного параметра tне зависит от эволюции, предшествовавшей t, при условии, что значение процесса в этот момент фиксировано (короче: "будущее" н "прошлое" процесса не зависят друг от друга при известном "настоящем").
Определяющее М. п. свойство принято наз. марковским; впервые оно было сформулировано А. А. Марковым [1]. Однако уже в работе Л. Башелье [2] можно усмотреть попытку трактовать броуновское движение как М. п., попытку, получившую обоснование после исследований Н. Винера (N. Wiener, 1923). Основы общей теории М. п. с непрерывным временем были заложены А. Н. Колмогоровым [3].
Марковское свойство. Имеются существенно отличающиеся друг от друга определения М. п. Одним из наиболее распространенных является следующее. Пусть на вероятностном пространстве  задан случайный процесс
задан случайный процесс  со значениями из измеримого пространства
со значениями из измеримого пространства  где Т - подмножество действительной оси
где Т - подмножество действительной оси  Пусть Nt (соответственно Nt).есть s-алгебра в
Пусть Nt (соответственно Nt).есть s-алгебра в  порожденная величинами X(s).при
порожденная величинами X(s).при  где
где  Другими словами, Nt (соответственно Nt) - это совокупность событий, связанных с эволюцией процесса до момента t(начиная с t). Процесс X(t).наз. марковским процессом, если (почти наверное) для всех
Другими словами, Nt (соответственно Nt) - это совокупность событий, связанных с эволюцией процесса до момента t(начиная с t). Процесс X(t).наз. марковским процессом, если (почти наверное) для всех  выполняется марковское свойство:
выполняется марковское свойство:

или, что то же самое, если для любых


М. п., для к-рого Тсодержится в множестве натуральных чисел, наз. Маркова цепью (впрочем, последний термин чаще всего ассоциируется со случаем не более чем счетного Е). Если Тявляется интервалом в  а Ене более чем счетно, М. п. наз. цепью Маркова с непрерывным временем. Примеры М. п. с непрерывным временем доставляются диффузионными процессами и процессами с независимыми приращениями, в том числе пуассоновским и винеровским.
а Ене более чем счетно, М. п. наз. цепью Маркова с непрерывным временем. Примеры М. п. с непрерывным временем доставляются диффузионными процессами и процессами с независимыми приращениями, в том числе пуассоновским и винеровским.
В дальнейшем для определенности речь будет идти только о случае  Формулы (1) и (2) дают ясную интерпретацию принципа независимости "прошлого" и "будущего" при известном "настоящем", но основанное на них определение М. п. оказалось недостаточно гибким в тех многочисленных ситуациях, когда приходится рассматривать не одно, а набор условий типа (1) или (2), отвечающих различным, хотя и согласованным определенным образом, мерам
Формулы (1) и (2) дают ясную интерпретацию принципа независимости "прошлого" и "будущего" при известном "настоящем", но основанное на них определение М. п. оказалось недостаточно гибким в тех многочисленных ситуациях, когда приходится рассматривать не одно, а набор условий типа (1) или (2), отвечающих различным, хотя и согласованным определенным образом, мерам  Такого рода соображения привели к принятию следующего определения (см. [9], [11]).
Такого рода соображения привели к принятию следующего определения (см. [9], [11]).
Пусть заданы:
а) измеримое пространство  где s-алгебра
где s-алгебра  содержит все одноточечные множества в Е;
содержит все одноточечные множества в Е;
б) измеримое пространство  снабженное семейством s-алгебр
снабженное семейством s-алгебр  таких, что
таких, что  если
если 
в) функция ("траектория") xt=xt(w), определяющая при любых  измеримое отображение
измеримое отображение 
г) для каждых  и
и  вероятностная мера
вероятностная мера  на s-алгебре
на s-алгебре  такая, что функция
такая, что функция 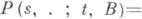
 измерима относительно
измерима относительно  если
если  и
и 
Набор  наз. (необрывающимся) марковским процессом, заданным в
наз. (необрывающимся) марковским процессом, заданным в  если
если  -почти наверное
-почти наверное

каковы бы ни были  Здесь
Здесь  - пространство элементарных событий,
- пространство элементарных событий,  - фазовое пространство или пространство состояний, Р(s, x, t, В) - переходная функция или вероятность перехода процесса X(t). Если Енаделено топологией, а
- фазовое пространство или пространство состояний, Р(s, x, t, В) - переходная функция или вероятность перехода процесса X(t). Если Енаделено топологией, а  - совокупность борелевских множеств в Е, то принято говорить, что М. п. задан в Е. Обычно в определение М. п. включают требование, чтобы
- совокупность борелевских множеств в Е, то принято говорить, что М. п. задан в Е. Обычно в определение М. п. включают требование, чтобы  и тогда
и тогда  истолковывается как вероятность
истолковывается как вероятность  при условии, что xs=x.
при условии, что xs=x.
Возникает вопрос: всякую ли марковскую переходную функцию Р(s, x; t, В), заданную в измеримом пространстве  можно рассматривать как переходную функцию нек-рого М. п. Ответ положителен, если, напр., Еявляется сепарабельным локально компактным пространством, а
можно рассматривать как переходную функцию нек-рого М. п. Ответ положителен, если, напр., Еявляется сепарабельным локально компактным пространством, а  - совокупностью борелевских множеств в Е. Более того, пусть Е - полное метрич. пространство и пусть
- совокупностью борелевских множеств в Е. Более того, пусть Е - полное метрич. пространство и пусть
 для любого
для любого  где
где  а
а  - дополнение e-окрестности точки х. Тогда соответствующий М. п. можно считать непрерывным справа и имеющим пределы слева (т. е. таковыми можно выбрать его траектории). Существование же непрерывного М. п. обеспечивается условием
- дополнение e-окрестности точки х. Тогда соответствующий М. п. можно считать непрерывным справа и имеющим пределы слева (т. е. таковыми можно выбрать его траектории). Существование же непрерывного М. п. обеспечивается условием 
 при
при  (см. [9], [11]). В теории М. п. основное внимание уделяется однородным (по времени) процессам. Соответствующее определение предполагает заданной систему объектов а) - г) с той разницей, что для фигурировавших в ее описании параметров sи u теперь допускается лишь значение 0. Упрощаются и обозначения:
(см. [9], [11]). В теории М. п. основное внимание уделяется однородным (по времени) процессам. Соответствующее определение предполагает заданной систему объектов а) - г) с той разницей, что для фигурировавших в ее описании параметров sи u теперь допускается лишь значение 0. Упрощаются и обозначения:
Далее, постулируется однородность пространства W, т. е. требуется, чтобы для любых  существовало такое
существовало такое  что
что  (w) при
(w) при  Благодаря этому на s-алгебре N, наименьшей из s-алгебр в W, содержащих любое событие вида
Благодаря этому на s-алгебре N, наименьшей из s-алгебр в W, содержащих любое событие вида  задаются операторы временного сдвига qt, к-рые сохраняют операции объединения, пересечения и вычитания множеств и для к-рых
задаются операторы временного сдвига qt, к-рые сохраняют операции объединения, пересечения и вычитания множеств и для к-рых

где

Набор  наз. (необрывающимся) однородным марковским процессом, заданным в
наз. (необрывающимся) однородным марковским процессом, заданным в  если
если  -почти наверное
-почти наверное

для  Переходной функцией процесса X(t).считается Р(t, x, В), причем, если нет специальных оговорок, дополнительно требуют, чтобы
Переходной функцией процесса X(t).считается Р(t, x, В), причем, если нет специальных оговорок, дополнительно требуют, чтобы 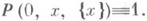 Полезно иметь в виду, что при проверке (4) достаточно рассматривать лишь множества
Полезно иметь в виду, что при проверке (4) достаточно рассматривать лишь множества  вида
вида  где
где  и что в (4) всегда Ft можно заменить s-алгеброй
и что в (4) всегда Ft можно заменить s-алгеброй  , равной пересечению пополнений Ft по всевозможным мерам
, равной пересечению пополнений Ft по всевозможным мерам  Нередко в
Нередко в  фиксируют вероятностную меру m ("начальное распределение") и рассматривают марковскую случайную функцию
фиксируют вероятностную меру m ("начальное распределение") и рассматривают марковскую случайную функцию  где
где  - мера на
- мера на  заданная равенством
заданная равенством

М. п.  наз. прогрессивно измеримым, если при каждом t>0 функция
наз. прогрессивно измеримым, если при каждом t>0 функция  индуцирует измеримое отображение
индуцирует измеримое отображение  в
в  где
где  есть s-алгебра
есть s-алгебра
борелевских подмножеств в [0, t]. Непрерывные справа М. п. прогрессивно измеримы. Существует способ сводить неоднородный случай к однородному (см. [11]), и в дальнейшем речь будет идти об однородных М. п.
Строго марковское свойство. Пусть в измеримом пространстве  задан М. п.
задан М. п.
Функция  наз. марковским моментом, если
наз. марковским моментом, если  для всех
для всех  При этом множество
При этом множество  относят к семейству Ft, если
относят к семейству Ft, если  при
при  (чаще всего Ft интерпретируют как совокупность событий, связанных с эволюцией X(t).до момента т). Для
(чаще всего Ft интерпретируют как совокупность событий, связанных с эволюцией X(t).до момента т). Для  полагают
полагают

Прогрессивно измеримый М. п. Xназ. строго марковским процессом (с. м. п.), если для любого марковского момента т и всех  и
и  соотношение
соотношение

(строго марковское свойство) выполняется 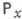 -почти наверное на множестве Wt. При проверке (5) достаточно рассматривать лишь множества вида
-почти наверное на множестве Wt. При проверке (5) достаточно рассматривать лишь множества вида  где
где  в этом случае
в этом случае  С. м. п. является, напр., любой непрерывный справа феллеровский М. п. в топологич. пространстве Е. М. п. наз. феллеровским марковским процессом, если функция
С. м. п. является, напр., любой непрерывный справа феллеровский М. п. в топологич. пространстве Е. М. п. наз. феллеровским марковским процессом, если функция

непрерывна всякий раз, когда f непрерывна и ограничена.
В классе с. м. п. выделяются те или иные подклассы. Пусть марковская переходная функция Р(t, x, В), заданная в метрическом локально компактном пространстве Е, стохастически непрерывна:

для любой окрестности Uкаждой точки  Тогда если операторы
Тогда если операторы  переводят в себя класс непрерывных и обращающихся в 0 в бесконечности функций, то функции Р(t, х, В).отвечает стандартный М. п. X, т. е. непрерывный справа с. м. п., для к-рого
переводят в себя класс непрерывных и обращающихся в 0 в бесконечности функций, то функции Р(t, х, В).отвечает стандартный М. п. X, т. е. непрерывный справа с. м. п., для к-рого

при

при
 и
и  - почти наверное на множестве
- почти наверное на множестве 

где
 а
а  - неубывающие с ростом пмарковские моменты.
- неубывающие с ростом пмарковские моменты. Обрывающийся марковский процесс. Нередко физич. системы целесообразно описывать с помощью необрывающегося М. п., но лишь на временном интервале случайной длины. Кроме того, даже простые преобразования М. п. могут привести к процессу с траекториями, заданными на случайном интервале (см. Функционал от марковского процесса). Руководствуясь этими соображениями, вводят понятие обрывающегося М. п.
Пусть  - однородный М. п. в фазовом пространстве
- однородный М. п. в фазовом пространстве  имеющий переходную функцию
имеющий переходную функцию  и пусть существуют точка
и пусть существуют точка  и функция
и функция  такие, что
такие, что  при
при  и
и  в противном случае (если нет специальных оговорок, считают
в противном случае (если нет специальных оговорок, считают  ). Новая траектория xt(w) задается лишь для
). Новая траектория xt(w) задается лишь для  ) посредством равенства
) посредством равенства  a Ft определяется как след
a Ft определяется как след  в множестве
в множестве 
Набор  где
где  наз. обрывающимся марковским процессом (о. м. п.), полученным из
наз. обрывающимся марковским процессом (о. м. п.), полученным из  с помощью обрыва (или убивания) в момент z. Величина z наз. моментом обрыва, или временем жизни, о. м. п. Фазовым пространством нового процесса служит
с помощью обрыва (или убивания) в момент z. Величина z наз. моментом обрыва, или временем жизни, о. м. п. Фазовым пространством нового процесса служит  где
где  есть след s-алгебры
есть след s-алгебры  в Е. Переходная функция о. м. п.- это сужение
в Е. Переходная функция о. м. п.- это сужение  на множество
на множество 
 Процесс X(t).наз. строго марковским процессом, или стандартным марковским процессом, если соответствующим свойством обладает
Процесс X(t).наз. строго марковским процессом, или стандартным марковским процессом, если соответствующим свойством обладает  Необрывающийся М. п. можно рассматривать как о. м. п. с моментом обрыва
Необрывающийся М. п. можно рассматривать как о. м. п. с моментом обрыва  Неоднородный о. м. п. определяется аналогичным образом. М. Г. Шур.
Неоднородный о. м. п. определяется аналогичным образом. М. Г. Шур.
Марковские процессы и дифференциальные уравнения. М. п. типа броуновского движения тесно связаны с дифференциальными уравнениями параболич. типа. Переходная плотность р(s, x, t, у).диффузионного процесса удовлетворяет при нек-рых дополнительных предположениях обратному и прямому дифференциальным уравнениям Колмогорова:

Функция р(s, x, t, у).есть функция Грина уравнений (6) - (7), и первые известные способы построения диффузионных процессов были основаны на теоремах существования этой функции для дифференциальных уравнений (6) - (7). Для однородного по времени процесса оператор L(s, x) = L(x).на гладких функциях совпадает с характеристич. оператором М. п. (см. Переходных операторов полугруппа).
Математич. ожидания различных функционалов от диффузионных процессов служат решениями соответствующих краевых задач для дифференциального уравнения (1). Пусть  - математич. ожидание по мере
- математич. ожидание по мере  Тогда функция
Тогда функция  удовлетворяет при s<T уравнению (6) и условию
удовлетворяет при s<T уравнению (6) и условию

Аналогично, функция

удовлетворяет при s<T уравнению

и условию и 2( Т, x) = 0.
Пусть тt - момент первого достижения границы дD области  траекторией процесса
траекторией процесса 
 Тогда при нек-рых условиях функция
Тогда при нек-рых условиях функция

удовлетворяет уравнению

и принимает значения ср на множестве

Решение 1-й краевой задачи для общего линейного параболич. уравнения 2-го порядка

при довольно общих предположениях может быть записано в виде

В случае, когда оператор Lи функции с, f не зависят от s, аналогичное (9) представление возможно и для решения линейного эллиптич. уравнения. Точнее, функция

при нек-рых предположениях есть решение задачи

В случае, когдгг оператор Lвырождается (del b(s, х) = 0).или граница дD недостаточно "хорошая", граничные значения могут и не приниматься функциями (9), (10) в отдельных точках или на целых множествах. Понятие регулярной граничной точки для оператора L имеет вероятностную интерпретацию. В регулярных точках границы граничные значения достигаются функциями (9), (10). Решение задач (8), (11) позволяет изучать свойства соответствующих диффузионных процессов и функционалов от них.
Существуют методы построения М. п., не опирающиеся на построение решений уравнений (6), (7), напр. метод стохастических дифференциальных уравнений, абсолютно непрерывная замена меры и др. Это обстоятельство вместе с формулами (9), (10) позволяет вероятностным путем строить и изучать свойства краевых задач для уравнения (8), а также свойства решении соответствующего эллиптич. уравнения.
Так как решение стохастического дифференциального уравнения нечувствительно к вырождению матрицы b(s, x), то вероятностные методы применялись для построения решений вырождающихся эллиптических и параболических дифференциальных уравнений. Распространение принципа усреднения Н. М. Крылова и Н. Н. Боголюбова на стохастические дифференциальные уравнения позволило с помощью (9) получить соответствующие результаты для эллиптических и параболических дифференциальных уравнений. Нек-рые трудные задачи исследования свойств решений уравнений такого типа с малым параметром при старшей производной оказалось возможным решить с помощью вероятностных соображений. Вероятностный смысл имеет и решение 2-й краевой задачи для уравнения (6). Постановка краевых задач для неограниченной области тесно связана с возвратностью соответствующего диффузионного процесса.
В случае однородного по времени процесса (Lне зависит от s) положительное решение уравнения  с точностью до мультипликативной постоянной совпадает при нек-рых предположениях со стационарной плотностью распределения М. п. Вероятностные соображения оказываются полезными и при рассмотрении краевых задач для нелинейных параболич. уравнений. Р. 3. Хасьминский.
с точностью до мультипликативной постоянной совпадает при нек-рых предположениях со стационарной плотностью распределения М. п. Вероятностные соображения оказываются полезными и при рассмотрении краевых задач для нелинейных параболич. уравнений. Р. 3. Хасьминский.
Лит.:[1] Марков А. А., "Изв. физ.-мат. об-ва Казан. ун-та", 1906, т. 15, №4, с. 135-56; [2] В а с h e l i е r L., "Ann. scient. Ecole norm, super.", 1900, v. 17, p. 21-86; [3] Колмогоров А. Н., "Math. Ann.", 1931, Bd 104, S. 415- 458; рус. пер.-"Успехи матем. наук", 1938, в. 5, с. 5-41; [4] Ч ж у н К а й - л а й, Однородные цепи Маркова, пер. с англ., М., 1964; [5] Р е 1 1 е r W., "Ann. Math.", 1954, v. 60, p. 417-36; [6] Д ы н к и н Е. Б., Ю ш к е в и ч А. А., "Теория вероятн. и ее примен.", 1956, т. 1, в. 1, с. 149-55; [7] X а н т Дж.-А., Марковские процессы и потенциалы, пер. с англ., М., 1962; [8] Д е л л а ш е р и К., Емкости и случайные процессы, пер. с франц., М., 1975; [9] Д ы н к и н Е. В., Основания теории марковских процессов, М., 1959; [10] его же, Марковские процессы, М., 1963; [11] Г и х м а н И. И., С к о р о х о д А. В., Теория случайных процессов, т. 2, М., 1973; [12] Фрейдлин М. И., в кн.: Итоги науки. Теория вероятностей, математическая статистика. - Теоретическая кибернетика. 1966, М., 1967, с. 7-58; [13] X а с ь м и н с к и й Р. 3., "Теория вероятн. и ее примен.", 1963, т. 8, в .1, с. 3-25; [14] Вентцель А. Д., Фрейдлин М. И., Флуктуации в динамических системах под действием малых случайных возмущений, М., 1979; [15] Blumenthal R. М., G e t о о r R. К., Markov processes and potential theory, N.Y.- L., 1968; [16] Getоor R. K., Markov processes: Ray processes and right processes, В., 1975; [17] Кузнецов С. Е., "Теория вероятн. и ее примен.", 1980, т. 25, в. 2, с. 389-93.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.