Akademik

топологическая группа, в к-рой групповые операции определены лишь для элементов, достаточно близких к единице. Введение Л. т. г. было инспирировано изучением локальной структуры топологич. групп (т. е. их структуры в сколь угодно малой окрестности единицы) (см. [1]). Точное определение Л. т. г. состоит в следующем.

Пусть G - топологич. пространство, е - нек-рый его элемент, - нек-рые открытые подмножества в G и соответственно, __ - нек-рые непрерывные отображения. Тогда система наз. Л. т. г., если выполнены условия:

Обычно Л. т. г. обозначают просто через G;элемент m((g, h)).обозначают через gh и наз. произведением gи h;элемент i(g).обозначают через g^-1 и наз. обратным к g; элемент еназ. единицей Л. т. г. G. Если то говорят, что произведение gи h определено; если то говорят, что для gопределен обратный элемент.

Эти (определенные не для любых элементов) одера-ции на Gиндуцируют структуру Л. т. г. на любой окрестности единицы ев G. Пусть G₁ и G₂- две Л. т. г. Локальным гомоморфизмом G₁ в G₂ наз. такое непрерывное отображение f нек-рой окрестности U₁ единицы е ₁ Л. т. г. С ₁ в нек-рую окрестность U₂ единицы е ₂ Л. т. г. G₂, что f(e₁)=e₂ и для любых элементов g,. произведение к-рых в GJ определено, произведение элементов f(g).и f(h).в G₂ также определено и Два локальных гомоморфизма G₁ в G₂ наз. эквивалентными, если они совпадают в нек-рой окрестности единицы Л. т. г. G₁. Пусть локальный гомоморфизм f является гомеоморфизмом окрестностей U₁ и U₂, а обратное отображение 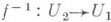является локальным гомоморфизмом Л. т. г. G₂ в Л. т. г. G₁. Тогда f наз. локальным изоморфизмом Л. т. г. G₁ и Л. т. г. G₂. Две Л. т. г., между к-рыми существует локальный изоморфизм, наз. локально изоморфными. Напр., любая Л. т. г. локально изоморфна любой своей окрестности единицы.

Примером Л. т. г. может служить любая топологич. группа (и, значит, любая ее окрестность единицы). В теории Л. т. г. принципиальным является вопрос о том, насколько общий характер имеет этот пример, т. е. является ли всякая Л. т. г. локально изоморфной некоторой топологич. группе. В общем случае ответ отрицателен (см. [4]), но в важном частном случае конечномерных Ли локальных групп - положителен.

Как и в теории топологич. групп, в теории Л. т. г. можно определить понятия (локальных) подгрупп, нормальных делителей, смежных классов, факторгрупп. Напр., пусть - Л. т. г., и Н - такое подмножество в G содержащее е, что в нек-рой окрестности Uединицы е Е G множество замкнуто. Пусть также для любого элемент i(g).принадлежит Н. а множество

открыто в (в предположении, что Нснабжено топологией, индуцированной с G). Тогда система

является Л. т. г., к-рая наз. локальной подгруппой в Л. т. г. G. Определения нормального делителя, смежных классов по подгруппе, факторгруппы см. в [1].

Лит.:[1] Понтрягин Л. С., Непрерывные группы, 3 изд., М., 1973; [2] Б у р б а к и Н., Группы и алгебры Ли. Алгебры Ли, свободные алгебры Ли и группы Ли, пер. с франц., М., 1976; [3] С е р р Ж.-П., Алгебры Ли и группы Ли, пер. с англ, и франц., М., 1969; [4] Lie S., Engel F., Theorie der Transformationsgruppen, 2 Aufl., Bd 1-3, Lpz., 1930.

В. Л. Попов.