Akademik

числа Nпо основанию а - показатель степени т, в к-рую следует возвести число "(основание Л.), чтобы получить N;обозначается log_aN, т. е. m=log_aN, если a^m=N. Каждому положительному числу соответствует при данном основании единственный действительный Л. (Л. отрицательных чисел являются комплексными числами). Основные свойства Л.:

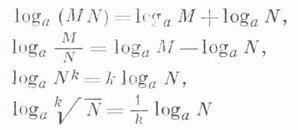
позволяют сводить умножение и деление чисел к сложению и вычитанию их Л., а возведение в степень и извлечение корня - к умножению и делению Л. на показатель степени или корня.

В соответствии с десятичным характером счета наиболее употребительны десятичные Л. (а=10), обозначаемые lg N. Для рациональных чисел, отличных от 10^k с целым k, десятичные Л. суть трансцендентные числа, к-рые приближенно выражают в конечных десятичных дробях. Целую часть десятичного Л. наз. характеристикой, дробную - мантиссой. Так как 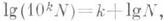то десятичные Л. чисел, отличающихся множителем 10*, имеют одинаковые мантиссы и различаются лишь характеристиками. Это свойство лежит в основе построения таблиц Л., к-рые содержат лишь мантиссы Л. целых чисел.

Большое значение имеют также натуральные Л., основанием к-рых служит трансцендентное число e=2,71828...; их обозначают ln N. Переход от одного основания Л. к другому совершается по формуле множитель 1/log_a bназ. модулем перехода (перевода) от основания ак основанию b. Формулы перехода от натуральных Л. к десятичным или обратно: ,

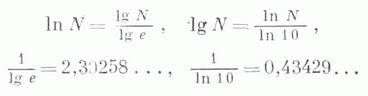
См. также Логарифмическая функция.

По материалам одноименной статьи из БСЭ-3.