Akademik

теорема, устанавливающая условия асимптотич. нормальности функции распределения суммы независимых случайных величин, обладающих конечными дисперсиями. Пусть X₁, Х₂, ...- последовательность независимых случайных величин с математич. ожиданиями а ₁, а ₂, . . . и конечными дисперсиями не все из к-рых равны нулю. Пусть

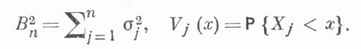
Для того чтобы

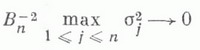
и

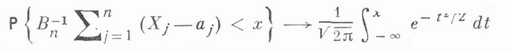
для любого хпри необходимо и достаточно выполнение следующего условия (условия Л и н д е б е р г а):

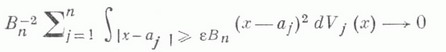
при для любого Достаточность была доказана Дж. Линдебергом [1], необходимость - В. Феллером [2].

Лит.:[1] L i n d е b е r g J. W., "Math. Z.", 1922, Bd 15, S. 211-25; [2] Feller W., "Math. Z.", 1935, Bd 40, S. 521 - 559; [3] Л о э в М., Теория вероятностей, пер. с англ., М., 1962; [4] П е т р о в В. В., Суммы независимых случайных величин, М., 1972. В. В. Петров.