Akademik

- фундаментальная форма Кэлера метрики па комплексном многообразии. К., ф. является гармонической вещественной дифференциальной формой типа (1, 1). Дифференциальная форма w на комплексном многообразии Мслужит К. ф. для нек-рой кэлеровой метрики тогда и только тогда, когда со в окрестности Uкаждой точки записывается в виде

где р - строго плюрисубгармонич. функция в 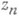- локальные комплексные координаты.

К. ф. наз. формой Ходжа, если она соответствует метрике Ходжа, т. е. имеет целочисленные периоды или, что то же, определяет целочисленный класс когомологий.

Лит.:[1] Уэллс Р., Дифференциальное исчисление на комплексных многообразиях, пер. с англ., М., 1976. А. Л. Онищик.