интеграл по кривой. Пусть в тг-мерном евклидовом пространстве 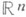 задана спрямляемая кривая
задана спрямляемая кривая 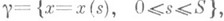
 - длина дуги и на кривой g задана функция F=F(x(s)). К. и.
- длина дуги и на кривой g задана функция F=F(x(s)). К. и.

определяется равенством
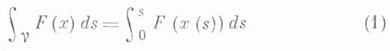
(справа - интеграл по отрезку) и наз. криволинейным интегралом первого рода, или криволинейным интегралом по длине дуги. Он является пределом соответствующих интегральных сумм, к-рые могут быть описаны в терминах, связанных с кривой. Напр., если функция F(x(s)).интегрируема по Риману (см. Римана интеграл),  - разбиение отрезка
- разбиение отрезка 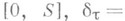
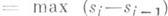
 - его мелкость,
- его мелкость, 
 - длина части кривой g от точки x(si-1). до точки
- длина части кривой g от точки x(si-1). до точки  и
и
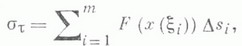
то
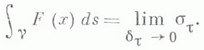
Если спрямляемая кривая g задана параметрическим представлением , и на ней задана функция F=F(x(t)), то интеграл
и на ней задана функция F=F(x(t)), то интеграл
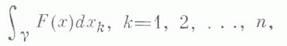
определяется равенством

(справа - Стилтъеса интеграл).и наз. к р и в о л и-нейным интегралом второго рода, или криволинейным интегралом по координате х k. Он также является пределом соответствующих интегральных сумм: если 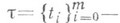 разбиение отрезка
разбиение отрезка 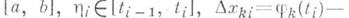
 и
и

то

Если F - непрерывная на спрямляемой кривой функция, то К. и. (1) и (2) всегда существуют. Если А- начало, а В- конец кривой g, то К. и. (1) и (2) обозначаются также через

К. и. первого рода не зависит от ориентации кривой:
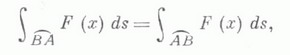
а К. и. второго рода меняет знак при изменении ориентации кривой:
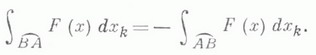
Если g - непрерывно дифференцируемая кривая, 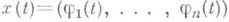 - ее непрерывно дифференцируемое представление,
- ее непрерывно дифференцируемое представление, 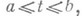 и F - непрерывная на g функция, то
и F - непрерывная на g функция, то
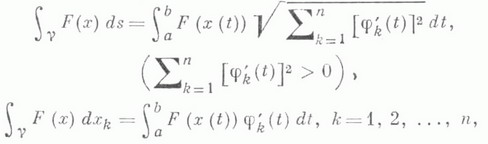
и тем самым интегралы, стоящие в правой части этих равенств, не зависят от выбора параметра на кривой g. Если  - единичный касательный вектор к кривой g, то К. н. второго рода выражается через К. и. первого рода по формуле
- единичный касательный вектор к кривой g, то К. н. второго рода выражается через К. и. первого рода по формуле
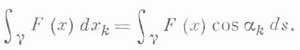
Если кривая g задана векторным представлением 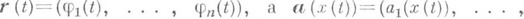
 - векторная функция, определенная на g, то, по определению,
- векторная функция, определенная на g, то, по определению,
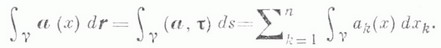
Связь между К. и. и интегралами других видов устанавливается Грина формулой и Стокса формулой.
С помощью К. и. можно вычислять площади плоских областей: если конечная плоская область Gограничена спрямляемым простым контуром g, то ее площадь равна
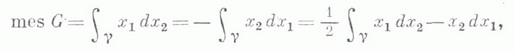
где контур g ориентирован против часовой стрелки. Если вдоль кривой g распределена нек-рая масса Мс линейной плотностьюr(x) , то
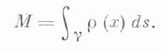
Если F(х) - напряженность силового поля (т. е. сила, действующая на единицу массы), тогда

равен работе силового поля вдоль кривой Y при перемещении вдоль g единичной массы. К. и. используются в теории векторных полей. Если непрерывное векторное поле 
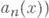 определено на нек-рой л-мерной области G, n>1, то следующие три свойства эквивалентны.
определено на нек-рой л-мерной области G, n>1, то следующие три свойства эквивалентны.
1) Для любой замкнутой спрямляемой кривой 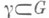 справедливо равенство
справедливо равенство 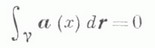 (векторное поле, обладающее этим свойством, наз. потенциальным).
(векторное поле, обладающее этим свойством, наз. потенциальным).
2) Для любой пары точек  и для любых двух спрямляемых кривых
и для любых двух спрямляемых кривых 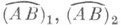 с началом в точко Аи концом в точке В:
с началом в точко Аи концом в точке В:

3) В области Gсуществует такая функция и(х).(называемая потенциальной функцией векторного поля а(х)), что  т. е.
т. е.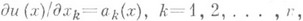 при этом для любых
при этом для любых 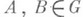 и любой кривой
и любой кривой 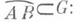
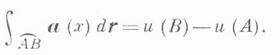
Если n=2 или n=3 и область Gодносвязна при n=2 и поверхностно односвязна при п=3, а поле  непрерывно дифференцируемо, то свойства 1) - 3) эквивалентны следующему свойству.
непрерывно дифференцируемо, то свойства 1) - 3) эквивалентны следующему свойству.
4) Вихрь векторного поля в области G равен нулю:

Если условие односвязности области G не выполнено, то свойство 4) не эквивалентно, вообще говоря, свойствам 1) - 3). Напр., для поля
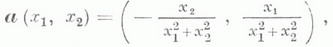
определенного на плоскости с выброшенным началом координат, имеем 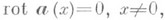 но
но

Лит.:[1] Ильин В. А., П о з н я к Э. Г., Основы математического анализа, 2 изд., ч. 2, М., 1980; [2] Кудрявцев Л. Д., Курс математического анализа, т. 2, М., 1981; [3] Никольский С. М., Курс математического анализа, 2 изд., т. 2, М., 1975. Л. Д. Кудрявцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.