Akademik

- определенный интеграл от функции нескольких переменных. Имеются различные понятия К. и. (интеграл Римана, интеграл Лебега, интеграл Лебега - Стилтьеса и др.).

Кратный интеграл Римана вводится на основе Жордана меры 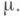Пусть Е- измеримое по Жордану множество n-мерного евклидова пространства есть n-мерная мера Жордана и - разбиение множества Е, т. е. такая система измеримых по Жордану множеств E_i, что 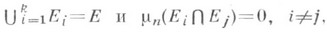Величину

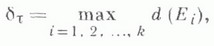
где d(E_i) - диаметр множества Е _i, наз. мелкостью разбиения 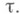Если функция определена на множестве Е, то всякую сумму вида

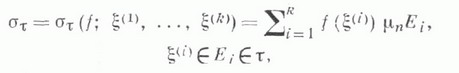
наз. интегральной суммой Римана функции f. Если для функции f существует 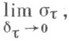независящий от разбиения, то этот предел наз. n-к ратным интегралом Римана и обозначают

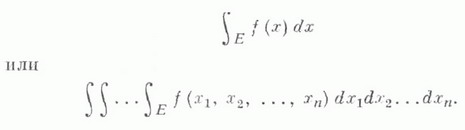
Саму функцию fназ. в этом случае интегрируемой по Риману, короче - R-интегрируемой.

В случае n=1 в качестве множества Е, по к-рому производится интегрирование, обычно берется отрезок, а в качестве его разбиений t рассматриваются разбиения, состоящие также только из отрезков (см. Римана интеграл). Таким образом, в этом случае как множество, по к-рому производится интегрирование, так и элементы разбиения представляют собой измеримые по Жордану множества весьма специального вида --отрезки. Поэтому не все свойства R-интегрируемых на отрезке функций справедливы для функций Д-интегрируемых на произвольных измеримых по Жордану множествах. Напр., из того, что любая функция, определенная на множестве жордановой меры нуль, Д-интегрируема на нем, следует, что Д-интегрируемые функции могут быть неограниченными, это невозможно для Д-интегрируемых функций на отрезках. Чтобы из Д-интегрируемости функции на нек-ром множестве следовала ограниченность функции, на рассматриваемое множество налагают дополнительные условия, напр, чтобы у него существовали сколь угодно мелкие разбиения, все элементы к-рых имеют положительную меру Жордана. К таким множествам относятся все измеримые по Жордану открытые множества и их замыкания, в частности измеримые по Жордану области и их замыкания. Имеь-но для таких множеств большей частью и используется кратный интеграл Римана.

В случае n=2 (n=3) К. и. наз. двойным (т р о й н ы м). Поскольку кратный интеграл Римана можно брать только по множествам, измеримым по Жордану (в случае n=2 они наз. также квадрируемыми, а при n=3 - кубируемыми множествами), то двойной (тройной) интеграл Римана рассматривают только на множествах (обычно областях или их замыканиях), границы к-рых имеют площади (объемы) в смысле Жордана, равные нулю.

Интеграл Римана от ограниченных функций n переменных обладает обычными свойствами интеграла (линейность, аддитивность относительно множеств, по к-рым производится интегрирование, сохранение при интегрировании нестрогих неравенств, интегрируемость произведения интегрируемых функций и т. п.).

Кратный интеграл Римана может быть сведен к повторному интегралу. Пусть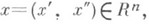

Е- измеримое в Rⁿ по Жордану множество,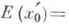 = 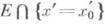- сечение множества Е(n-m)-мерной гиперплоскостью 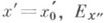- проекция Ена гиперплоскость 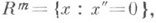причем 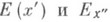измеримы соответственно в смысле (n-m)-мерной и m-мер-ной меры Жордана. Тогда, если функция f Д-интегрируема на множестве Еи для всех 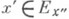существуют (n-m)-кратные интегралы от ее сужения на множестве 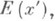то существует повторный интеграл

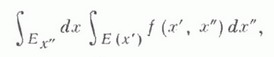
где внешний интеграл является m-кратным интегралом Римана, и

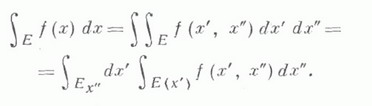
Для случая n=3 отсюда следуют формулы: 1) Если - проекция Eна плоскость а функции 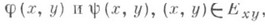таковы, что множество Еограничено в направлении оси z их графиками, т. е.

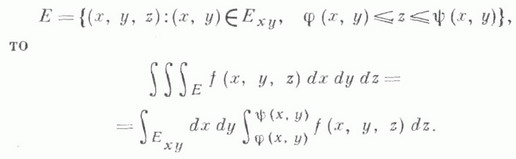
2) Пусть проекцией множества Ена ось Ох является отрезок - сечение множества Еплоскостью, параллельной плоскости 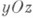и проходящей через точку х, тогда

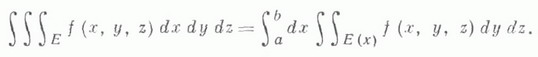
В случае, когда Gявляется измеримой по Жордану областью в пространстве 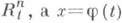- взаимно однозначное отображение G на измеримую область Г пространства 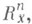причем 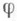непрерывно дифференцируемо на замыкании 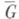области G, для интегрируемой на = 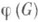функции f (х).справедлива формула замены переменного в интеграле

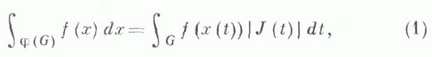
где J(t) - якобиан отображения j.

Геометрический смысл кратного интеграла Римана от функции ппеременных связан с понятием ( п+1)-мерной меры Жордана если функция f (х).интегрируема на множестве 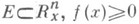на Еи

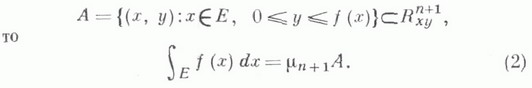
Кратным интегралом Лебега наз, Лебега интеграл от функций многих переменных, его определение базируется на понятии Лебега меры в n-мерном евклидовом пространстве. Кратный интеграл Лебега может быть сведен к повторному интегралу (см. Фубини теорема). Для непрерывно дифференцируемых взаимно однозначных отображений областей справедлива формула замены переменного (1), а также формула (2), выражающая геометрии, смысл кратного интеграла Лебега, в к-рой под мерой 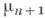следует понимать (n+1)-мерную меру Лебега.

Понятие К. и. переносится на функции, интегрируемые по множеству А, принадлежащему произведению пространств Xи У, в каждом из к-рых заданы 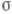-конечные полные неотрицательные меры, соответственно 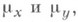при этом интегрирование по множеству Апроизводится по мере 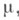являющейся произведением мер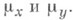

Для функций многих переменных существует также понятие несобственного К. и. (см. Несобственный интеграл). Понятие К. и. применяется также к неопределенным интегралам функций многих переменных. Под неопределенным К. и. понимают функцию множества

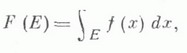
где Е - измеримое множество. Если, напр., f(x).интегрируема по Лебегу на нек-ром множестве, то ее неопределенный интеграл F(Е).почти всюду на этом множестве имеет функцию f(x).своей симметричной производной. В этом смысле (аналогично случаю функций одной переменной) взятие неопределенного К. и. является операцией, обратной к операции дифференцирования функции множества.

Лит.:[1] И л ь и н В. А., Лозняк Э. Г., Основы математического анализа, 2 изд., ч. 2, М., 1980; [2] К о л м о г о р о в А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 5 изд., М., 1981: [31 Никольский С, М., Курс математического анализа, 2 изд., т. 2, М., 1975. Л. Д. Кудрявцев.