Akademik

- гармоническая функция, у к-рой операторы Лапласа по отдельным группам независимых переменных обращаются в нуль. Точнее, функция класса 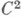в области Dевклидова пространства наз. К. ф. в D, если существуют такие натуральные числа что всюду в Dвыполняются тождества:

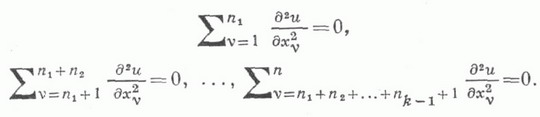
Важный собственный подкласс класса К. ф. составляют плюригармонические функции, для к-рых т. е. k=m, и к-рые, кроме того, удовлетворяют век-рым дополнительным условиям.

Лит.:[1] С т е й н И., В е й с Г., Введение в гармонический анализ на евклидовых пространствах, пер. с англ., М., 1974. Е. Д. Соломенцев.