Akademik

- интегральная предельная теорема для вероятностей больших отклонений (уклонений) сумм независимых случайных величин. Пусть Х ₁, Х ₂, ... - последовательность независимых случайных величин с общей невырожденной функцией распределения Р(х). такой, что 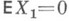и производящая функция моментов 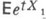конечна в нек-ром интервале |t|<H (последнее условие наз. условием Крамера). Пусть

Здесь Ф (х) - нормальная (0, 1) функция распределения, 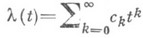- так наз. ряд Крамера, коэффициенты к-рого зависят только от моментов случайной величины Х ₁;этот ряд сходится для всех достаточно малых t. Несколько более слабый по сравнению с приведенным выше результат был получен Г. Крамером (Н. Сrаmer) в 1938.

Лит.:[1] К р а м е р Г., "Успехи матем. наук", 1944, в. 10, с. 166-78; [2] И б р а г и м о в И. А., Л и н н и к Ю. В., Независимые и стационарно связанные величины, М., 1965; [3] Петров В. В., Суммы независимых случайных величин, М., 1972. В. В. Петров.