Akademik

для эллиптического уравнения - задача отыскания регулярного в области Dрешения иэллиптического уравнения

удовлетворяющего нек-рым дополнительным условиям на границе Г области D. Классические К. з. являются частными случаями следующей задачи: найти регулярное в области Dрешение уравнения (1), удовлетворяющее на границе Г условию

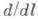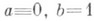где - производная по нек-рому направлению; а, Ь и g - заданные непрерывные на Г функции, причем всюду на Г (см. [1]). При К. з. есть Дирихле задача;при а=1 - задача с косой производной (см. Дифференциальное уравнение с частными производными;задача с косой производной), к-рая переходит в Неймана задачу, если направление l совпадает с направлением конормали. Если 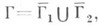где Г ₁ и Г ₂ - непересекающиеся открытые подмножества 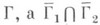либо является ( п-2)-мерным многообразием, либо пусто, и a=1, b=0 на Г ₁, а=0, b=1на Г ₂, то получается смешанная задача.

Задача (2) изучалась для эллиптич. уравнений с двумя независимыми переменными (см. [2]). Довольно полно исследованы задача Дирихле для эллиптич. уравнений с любым конечным числом независимых переменных (см. [1], [3], [4]) и задача с косой производной в том случае, когда направление lни в одной точке Г не выходит в касательную к Г плоскость. В этом случае задача с наклонной производной - фредгольмова и решение имеет такую же гладкость, как и поле направлений lи функция g(см. [1]). Изучался случай, когда lвыходит в касательную к Г плоскость в нек-рых точках Г (см. [3]). Были исследованы локальные свойства решений задачи с косой производной (см. [5]). В точках выхода поля lв касательную к Г плоскость решение задачи менее гладкое, чем поле lи функция g. На основании этого исследована задача в обобщенной постановке (см. [7], [8]).

Пусть краевое условие для регулярных в единичном шаре гармонич. функций имеет вид

К - множество точек единичной сферы S, в к-рых обращается в нуль функция 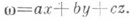Векторное поле Р( а, b, с) по множеству Квыходит в касательную к единичной сфере Sплоскость. Пусть, кроме того, Ксостоит из конечного числа непересекающихся кривых, 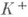- подмножество К, состоящее из таких точек, в к-рых grad w составляет острый угол с проекцией поля Рна сферу S, и К ^- - оставшаяся часть К. Обобщенная постановка задачи заключается в дополнительном задании значении и на K⁺ , но на множестве К ^- допускаются интегрируемые особенности у решения и. В случае, когда К ^- пусто, за счет повышения гладкости дополнительных данных задачи можно сделать сколь угодно гладким решение обобщенной задачи. Решение смешанной задачи на множестве вообще говоря, имеет особенности (см. [1]). Для того чтобы это решение не имело особенностей на Г ₀, необходимо накладывать дополнительные условия на данные задачи (см. [11]). Широкий класс К. з. составляют так наз. задачи со свободными границами. В этих задачах требуется найти не только решение уравнения (1), но и область его регулярности. Граница Г области неизвестна, но на ней должны удовлетворяться два краевых условия. Примером таких задач является задача о волновых движениях идеальной жидкости. В этой задаче ищется регулярная в нек-рой области Dгармонич. функция и, причем часть Г ₁ границы известна и на Г ₁ нормальная производная 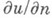равна нулю, а другая часть границы Г ₂ неизвестна и на ней выполняются два краевых условия:

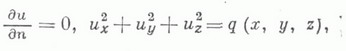
где q>0 - заданная функция.

Для гармонич. функций двух независимых переменных используется аппарат конформных отображений (см. [12], [13], [14]). См. также Дифференциальное уравнение с частными производными;задача со свободными границами. Исследовалась следующая задача: найти регулярную в области Dгармонич. функцию и, удовлетворяющую на границе Г области условию

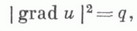
где q>0 - заданная функция. Для гармонич. функций двух независимых переменных эта задача решена полностью (см. [14]).

Для уравнения 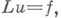где L - равномерно эллиптический в замыкании области Dоператор порядка 2т, рассматривается задача отыскания регулярного в Dрешения и, удовлетворяющего на границе Г области Dусловиям:

где 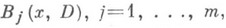- дифференциальные операторы, удовлетворяющие следующему условию дополнительности.

Пусть - главная часть оператора - главная часть оператора 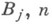- нормаль к Г в точке - произвольный вектор, параллельный Г. Через 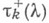обозначены корни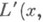 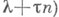с положительными мнимыми частями. Многочлены 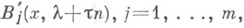относительно переменного 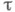должны быть линейно независимыми по модулю многочлена 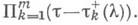И в этом случае задача является нормально разрешимой. Нарушение условия дополнительности может повлечь существенное изменение характера задачи (см. [17]).

Задача (2) - частный случай задачи (3). Для задачи (2) при условие дополнительности эквивалентно тому, что направление lни в одной точке границы области не выходит в касательную к границе плоскость.

Другим частным случаем задачи (3) является задача с краевыми условиями:

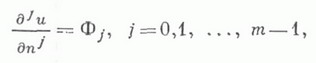
к-рая есть некоторый аналог задачи Дирихле для эллиптич. уравнений высших порядков. Изучена К. з. для полигармонич. уравнения 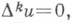когда граница области состоит из многообразий различной размерности (см. [15]). При исследовании К. з. для нелинейных уравнений (напр., задач Дирихле и Неймана) важную роль играют априорные оценки решений (1), различные принципы неподвижной точки (см. [17], [18]) и обобщения Морса теории, на бесконечномерный случай (см. [19]).

Лит.:[1] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957; [2] В е к у а И. Н., Обобщенные аналитические функции, М., 1959; [3] Бицадзе А. В., Краевые задачи для эллиптических уравнений второго порядка, М., 1966; [4] К е л д ы ш М. В., "Успехи матем. наук", 1941, в. 8, с. 171-292; [5] Н o r m a n d е r L., "Ann. Math.", 1966, v. 83, № 1, p.129-209; [6] В о r r е l l i R. L., "J. Math. and Mech.", 1966, v. 16, M 1, p. 51-81; [7] Eгopов Ю. В., К о н д р а т ь е в В. А., "Матем. сб.", 1969, т. 78, № 1, с. 148-76; [81 М а з ь я В. Г., "Матем. сб.", 1972, т. 87, № 3, с. 417-53; [9] Я н у ш а у с к а с А., "Докл. АН СССР", 1965, т. 164, №4, с. 753 - 55; [10J Вишик М. И., Э с к и н Г. И., "Сиб. матем. ж.", 1968, т. 9, № 5, с. 973-97; [11] G i r a u d G., "Ann. Soc. Polon. de Math., annee 1933", Krakow, 1934, t. 12, p. 35-54; [12] Л а в р е н т ь е в М. А., Вариационный метод в краевых задачах для систем уравнений эллиптического типа, М., 1962; [13] Некрасов А. И., Точная теория волн установившегося вида на поверхности тяжелой жидкости, в кн.: Собр. соч., т. 1, М., 1961; [14] Г а х о в Ф. Д., Краевые задачи, 2 изд., М., 1963; [15] Соболев С. Л., "Матем. сб.", 1937, т. 2, №3, с. 465-99; [16] А г м о н С., Дуглис А., Ниренберг Л., Оценки вблизи границы решений эллиптических уравнений в частных производных при общих граничных условиях, пер. с англ., М., 1962; [17] S с h a u d e r J., "Math. Z.". 1931, Bd 33, S. 602-40; [18] Leray J., Schauder J., "Ann. sci. Ecole norm. sup.", ser. 3, 1934, t. 51, p. 45-78; [19] P a 1 a i s R. S., "Topology", 1963, v. 2, № 4, p. 299-340. А. И. Янушаускас.