Akademik

для класса S - проблема для класса функций

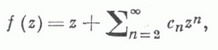
регулярных и однолистных в круге 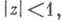заключающаяся в определении для каждого 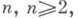области значений V_n системы коэффициентов {с ₂, с ₃, . . ., с _n} функций этого класса и, в частности, в нахождении точных оценок для в классе S(см. Бибербаха гипотеза). К. п. для нек-рого класса Rфункций, регулярных в заключается в определении в классе Л для каждого области значений системы первых пкоэффициентов разложения функции класса Л в ряд по степеням z и, в частности, в получении точных оценок этих коэффициентов в классе R. К. п. решена для Каратеодори класса, для класса регулярных типично вещественных в круге функций, для класса однолистных звездообразных функций, для класса функций, регулярных и ограниченных в

Известно, что V₂ - круг: Получены глубокие качественные результаты по К. п. в классе S(см. [7]). Множество V_n - ограниченная замкнутая область, точка _ внутренняя точка V_n; V_n гомеоморфно замкнутому (2n-2)-мерному шару; граница V_n состоит из конечного числа частей П ₁, П ₂, . . ., Пдт; координаты точки ( с ₂, с ₃, . . ., с _n).на любой одной из этих частей - функции конечного числа параметров 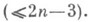Каждой граничной точке V_n соответствует единственная функция класса S. Граница V₃ состоит из двух гиперповерхностей П ₁ и П ₂ размерности 3 и их пересечения: поверхностей П ₃ и П ₄ и кривой П ₅. Для П ₁ и П ₂ получены параметрич. формулы в терминах элементарных функций. Сечение V₃ плоскостью Im с ₂=0 симметрично относительно плоскостей 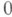и Im c₃=0. Сечение V₃ плоскостью 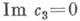симметрично относительно плоскосте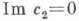й и 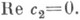Функция 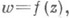соответствующая точке поверхности П ₁, отображает на плоскость w с единственным аналитич. разрезом, уходящим в бесконечность. Функция w=f(z), соответствующая точке поверхности П ₂, отображает 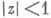на плоскость wс разрезом по трем аналитич. дугам, исходящим из нек-рой конечной точки под углом 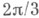друг к другу, одна из этих дуг лежит на прямой и уходит в бесконечность.

Были исследованы также: область значений {с ₂, с ₃} в подклассе функций из Sс действительными с ₂ и с ₃; области значений если 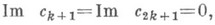на подклассе ограниченных функций из Sвида

область значений {с ₂, с ₃} на подклассе ограниченных функций из S;область значений {с ₂, с ₃, с ₄} в подклассе функций из Sс действительными с ₂, с ₃ и с ₄. Точные оценки для коэффициентов вида 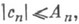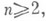получены в подклассе выпуклых функций из Sс A_n=1, в подклассе звездообразных функций из Sс А _п=п, в подклассе нечетных звездообразных функций из Sс А _п=1, n=3, 5, ..., в классе однолистных функций с действительными коэффициентами с А _п=п, в подклассе близких к выпуклым функций из Sс А _п=п. В классе функций

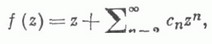
регулярных и типично вещественных в имеет место точная оценка а в классе Бибербаха - Эйленберга функций - точная оценка Для класса функций

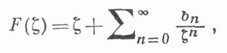
мероморфных и однолистных в 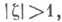известны точные оценки:

Для подкласса звездообразных функций из 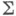справедлива точная оценка

Имеются точные оценки коэффициентов и в других подклассах из S и 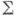(см. [1]-[4]), а также в нек-рых классах р-листных функций и в классах р-листных в среднем функций (см. [5]).

Лит.: [1] Г о л у з и н Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [2] Б а з и л е в и ч И. Е., в кн.: Математика в СССР за сорок лет. 1917- 1957, т. 1, М., 1959, с. 444-72; [3] Дженкинс Дж., Однолистные функции и конформные отображения, пер. с англ., М., 1962; [4] Н а у m a n W. К., "J. London Math. Soc.", 1965, v. 40, pt 3, p. 385-406; [5] G о о d m a n A. W., "Bull. Amer. Math. Soc.", 1968, v. 74, M 6, p. 1035-50; [6] P h e 1 p s D., "Trans. Amer. Math. Soc.", 1969, v. 143, p. 475-85; [7] S с h a e f f e r A. C., S p e n с е г D. C., Coefficient regions for schlicht functions, N. Y., 1950. E. Г. Голузина.