Akademik

в статистической механике - функция, описывающая влияние частиц или групп частиц друг на друга и эффекты взаимодействия подсистем рассматриваемой системы. В классической статистич. механике К. ф. G₂(l, 2), G₃(l, 2.3), ... определяются соотношениями

где символами 1, 2, ... в аргументах функций обозначена совокупность координат r и импульсов рсоответственно 1-й, 2-й, . . . частицы, F_s(l, . . ., s) - приведенные функции распределения

V - объем системы, N - число частиц, D_t=D_t(l, 2, ..., N) - функция распределения в фазовом пространстве в момент времени E с нормировкой

Закон изменения D_t во времени характеризуется уравнением Лиувилля 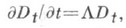в к-ром L представляет не зависящий явно от времени оператор Лиуйилля. Обычно рассматривается случай, когда L состоит из суммы аддитивной части и бинарной части, характеризующей взаимодействия между частицами:

Согласно принципу ослабления корреляции К. ф. удовлетворяют граничным условиям при max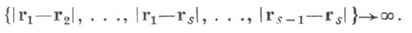

К. ф. являются функциональными производными функционала

A_t (и), связанного с так наз. производящим функционалом

Функционал A_t(u)удовлетворяет уравнению

В квантовой статистич. механике К. ф. являются операторными величинами и определяются соотношениями;

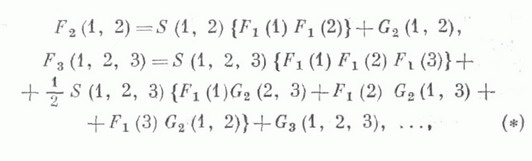
где S(1, 2), S(1, 2, 3) - операторы симметризации для бозе-систем и антисимметризации для ферми-систем. К. ф. (*), наз. матрицей плотности, удовлетворяет квантовомеханич. уравнению Лиувилля (см. [2]). В квантовой статистич. механике помимо К. ф. (*) рассматриваются К. ф., построенные на обычных термодинамических средних (см. [3]), и К. ф., построенные на квазисредних (см. [3]). Билинейные комбинации К. ф. (как квантовые, так и классические) дают функции Грина (см. [5]). Для К. ф. справедливы спектральные представления, Боголюбова неравенство, вариации среднего значения теорема (см. [4]). Иногда используют К. ф., соответствующие так наз. разложению Кирквуда (см. [6]); пространственно-временную К. ф. (см. [8]). К. ф. могут быть интерпретированы как характеристики вероятностных мер (см. [9]).

Лит.:[1] Б о г о л ю б о в Н. Н., Проблемы динамической теории в статистической физике, М.- Л., 1946; 12] Б о г о л ю б о в Н. Н., Г у р о в К. П., "Ж. экспериментальной и теоретич. физики", 1947, т. 17, в. 7, с. 614-28; [3] Боголюбов Н. Н., Избранные труды, т. 3, К., 1971; [4] Боголюбов Н. Н., (м л.), Садовников Б. И., Некоторые вопросы статистической механики, М., 1975; [5] Б о г о л ю б о в Н. Н., Т я б л и к о в С. В., "Докл. АН СССР", 1959, т. 126, № 1, с. 53-56; [6] Л и б о в Р., Введение в теорию кинетических уравнений, пер. с англ., М., 1974; [7] И с и х а р а А., Статистическая физика, пер. с англ., М., 1973; [8] Р ю э л ь Д., Статистическая механика. Строгие результаты, пер. с англ., М., 1971; [9] П р е с т о н К. Дж., Гиббсовские состояния на счетных множествах, пер. с англ., М., 1977.

А. Н. Ермилов, А. М. Курбатов.