Akademik

- проективное n-пространство, в к-ром метрика определяется абсолютом, заданным совокупностью абсолютного конуса Q₀ индекса kс (n- т--1)-вершиной (абсолютная плоскость Т _а )и (n-m-2)-квадрикой (абсолютная квадрика Q₁) индекса lна этой (n-m-1)-плоскости. Определяемое таким образом пространство наз. кваз и гиперболическим пространством индексов kи l, обозначается символом 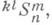где m<n. К. п. является частным случаем полугиперболических пространств. К. п. получается предельным переходом из гиперболич. пространства ^lS_n таким образом, что при этом абсолют гиперболич. пространства переходит в абсолют К. п.

При т=0 конус Q₀ является парой слившихся плоскостей, совпадающих с плоскостью Т ₀, а абсолют пространства совпадает с абсолютом псевдоевклидова пространства При т=1 конус Q₀ является парой действительных плоскостей; в частности, для плоскость Т ₀ является прямой пересечения этих двух плоскостей, а квадрика Q₁- парой точек на прямой Т ₀. В случае m=n-1 конус Q₀ имеет точечную вершину, и абсолют пространства совпадает с абсолютом копсевдоев клидова пространства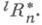

К. п. являются пространствами более общего проективного типа по отношению к копсевдоевклидовым пространствам.

Проективная метрика К. п.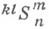определяется таким образом, чтобы при то=0 получалась метрика псевдоевклидова пространства а при т=п-1 - метрика копсевдоевклидова пространства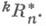

В К. п. различают прямые четырех типов: эллиптические прямые, пересекающие абсолютный конус в двух мнимо сопряженных точках; гиперболические прямые, пересекающие абсолютный конус в двух действительных точках; параболические прямые, проходящие через вершину абсолютного конуса; изотропные прямые, проходящие через вершину абсолютного конуса и касающиеся его.

Расстояние d между двумя точками Xи Yопределяется в случае, когда прямая XY не пересекается с (п-т-1)-плоскостью Т ₀, с помощью соотношения

где Е _о- линейный оператор, определяющий скалярное произведение в псевдоевклидовом (m+1)-пространстве , y⁰= ( у ^ь,)- векторы точек

Xи У, р - действительное число. Расстояние между двумя точками, не лежащими на параболич. прямой, равно расстоянию между проекциями этих точек на m-плоскость x¹=0 в направлении ( п- т-1)-плоскости Т ₀. В случае, когда прямая XY пересекает (n-m-1)-плоскость Т _а, то расстояние dвычисляется с помощью разности а= у¹-x¹, где x¹=( х ^и, u>m), y¹={y^u,u>m)- векторы точек Xи Y в псевдоевклидовом пространстве R_n-m; d(XY)=aE₁a, здесь E₁ - линейный оператор, определяющий скалярное произведение в этом пространстве.

За угол между двумя плоскостями пространства 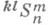принимается (нормированное) расстояние между двумя соответствующими точками в двойственном ему пространстве 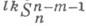по принципу двойственности проективного re-пространства. Координаты этих точек численно равны проективным координатам данных плоскостей. В случае, когда (п-2)-плоскость пересечения двух данных плоскостей пересекается с (п-m-1)-плоскостью Т ₀, этот угол всегда равен нулю, но тогда применяется способ измерения, аналогичный измерению расстояний в подобном случае. В частности, при n= 2 углы между 1-плоскостями являются углами между прямыми и, в зависимости от расположения 2-плоскости относительно плоскости Т ₀, на этой плоскости возможны три типа геометрий - евклидова, псевдоевклидова или копсевдоевклидова.

Движениями К. п. являются коллинеации, сохраняющие расстояние между точками и переводящие абсолютный конус Q₀,(n- m- 1)-вершину Т ₀ и (n-m-2)-квадрику Q₁ в Т ₀ в себя. Движения описываются псевдоортогональными операторами индекса 2. В К. п.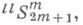 двойственном самому себе, определяется кодвижение - корреляция, переводящая всякие две точки в две плоскости, угол между к-рыми пропорционален расстоянию между двумя данными точками, а всякие две плоскости - в две точки, расстояние между которыми пропорционально углу между плоскостями. Кодвижения описываются псевдоортогональными операторами индекса I. Движения образуют группу Ли, как и движения и кодвижения двойственного самому себе К. п.

Квазигиперболическое 3-пространство с проективной Эллиптич. метрикой на прямых -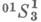- имеет коевклидову метрику на 2-плоскостях и псевдоевклидову метрику индекса 1 в связках плоскостей. Квазигиперболическое 3-пространство с гиперболической проективной метрикой расстояний может быть двух типов - 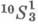и 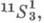отличающихся метриками в связках плоскостей: в первом - евклидова, во втором - псевдоевклидова метрика индекса 1. Метрика на 2-плоскостях одна и та же - копсевдоевклидова индекса 1.

Квазигиперболическое 3-пространство может быть интерпретировано как группа движений псевдоевклидовой 2-плоскости индекса 1. Многообразие гиперболич. прямых указанного квазигиперболического 3-пространства допускает интерпретацию на паре таких псевдоевклидовых плоскостей. Пространства и ⁰¹S¹₃, двойственные друг другу, допускают интерпретации на комплексной 2-плоскости.

Лит.:[1] Розенфельд Б. А., Неевклидовы пространства, М., 1969; [2] Яглом И. М., Розенфельд Б. А., Ясинская Е. У., "Успехи матем. наук", 1964, т. 19, в. 5, с. 51 - 113.

Л. А. Сидоров.