Akademik

- всякая система аксиом 2 , для к-рой все алгебраические системы сигнатуры 2, удовлетворяющие этим аксиомам, изоморфны. Из теоремы Мальцева - Тарского об элементарном расширении следует, что модели категоричной системы е аксиом 1-го порядка имеют конечную мощность. Верно и обратное: для любой конечной алгебраич. системы Асуществует категоричная система е аксиом 1-го порядка, модели к-рой изоморфны А. Пусть е ₀ - множество универсальных замыканий формул

где j(х).- любая формула сигнатуры 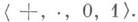Система аксиом е ₀ известна под названием арифметики Пеан о. Арифметика натуральных чисел N будет моделью для е ₀. Однако существуют модели е ₀, не изоморфные N. Пусть система е ₁ получается из е ₀ заменой схемы элементарной индукции 7) на аксиому полной индукции

записанную на языке 2-го порядка. Система е ₁ является категоричной, и все модели е ₁ изоморфны арифметике натуральных чисел N. Другой способ категоричного описания арифметики Nсостоит в добавлении к е ₀ следующей бесконечной аксиомы (языка L_w1w):

где п- сокращение для суммы 1+.. .+1 из пединиц.

Лит.:[1] Шенфилд Дж., Математическая логика, пер. с англ., М., 1975.

Е. А. Полютин.