Akademik

- специальная функция, определяемая для действительного х неравно 0 равенством

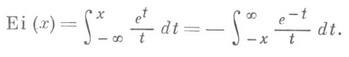
График И. п. ф. см. на рис.

При х>0 подинтегральная функция имеет бесконечный разрыв в точке х=0 и И. п. ф. понимается в смысле главного значения этого интеграла:

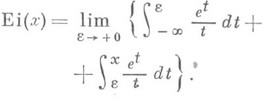
И. п. ф. представляется в виде рядов

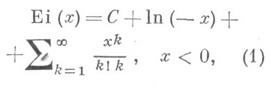
и

где С=0,5772...- Эйлера постоянная.

Имеет место асимптотическое представление:

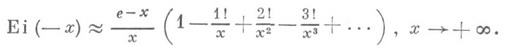
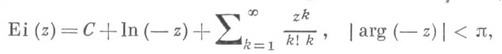
Как функция комплексного переменного z, И. п. ф. есть однозначная аналитич. функция в плоскости z с разрезом вдоль положительной действительной полуоси (0 <arg z<2p); значение ln(-z) выбирается при этом так, чтобы -p<Imln(-z)<p. Поведение Ei (z) вблизи разреза описывается предельными соотношениями:

Асимптотич. представление в области 0<argz<2p

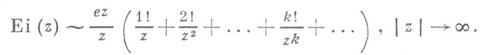
И. п. ф. связана с интегральным логарифмомli(х)соотношениями:

с интегральным синусомSi (x)и интегральным косинусомCi (x)соотношениями:

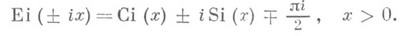
Формула дифференцирования:

Иногда используются обозначения

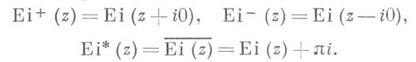
Лит.:[1] Бейтмен Г., Эрдейи А., Высшие трансцендентные функции. Функции Бесселя, функции параболического цилиндра, ортогональные многочлены, пер. с англ., 2 изд., М., 1974; [2] Янке Е., Эмде Ф., Лёш Ф., Специальные функции. Формулы, графики, таблицы, пер. с нем., 2 изд., М., 1968; [3] Кратцер А., Франц В., Трансцендентные функции, пер. с нем., М., 1963; [4] Лебедев Н. Н., Специальные функции и их приложения, 2 изд., М., 1963.