Akademik

гармоническое деление, деление в крайнем и среднем отношени и,- деление отрезка а, при к-ром большая часть хявляется средней пропорциональной между всем отрезком аи меньшей его частью а- х, то есть а: х = х:(а-х). (*)

Для нахождения хполучается квадратное уравнение x²+ax-a²=0, решение к-рого 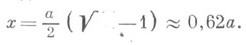дает

Условие (*) можно переписать и так

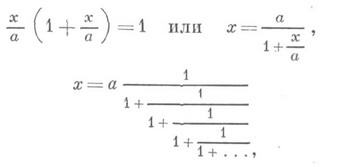
т. е. хполучают в виде непрерывной дроби, подходящие дроби к-рой будут:

тде 1, 1,2, 3, 5, 8, 13, 21 и т. д.- так наз. Фибоначчи числа.

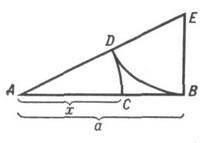
Геометрически 3. с. отрезка АВ (см. рис.) строится так: в точке Ввосстанавливают перпендикуляр к А В, откладывают на нем отрезок соединяют Аи Е, откладывают ED = EB и, наконец, AC=AD, тогда

АВ: АС=АС: СВ.

З. с. было известно еще в древности. В дошедшей до нас античной литературе 3. с. впервые встречается в "Началах" Евклида (3 в. до н. э.).

Термин "3. с." ввел Леонардо да Винчи (Leonardo da Vinci) (кон. 15 - нач. 16 вв.). Принципы 3. с. или близкие ему пропорциональные отношения легли в основу композиционного построения многих произведений мирового искусства (главным образом произведений архитектуры античности и Возрождения).