Akademik

для семейства распределений вероятностей {P_q; } или для параметра - статистика (векторная случайная величина) такая, что для любого события Асуществует вариант условной вероятности P_q( А|Х=x), не зависящий от 9. Это эквивалентно требованию, что условное распределение любой другой статистики У при условии Х = х не зависит от 9.

Знание Д. с. Xдает исчерпывающий материал для статистич. выводов о параметре 0, поскольку любые дополнительные статистич. данные ничего не добавляют к той информации о параметре, к-рая содержится в распределении X. Математич. выражением этого свойства является один из результатов теории статистич. решений, утверждающий, что множество решающих правил, основанных на Д. с, образует существенно полный класс. Переход от исходного семейства распределений к семейству распределений Д. с. наз. редукцией статистической задачи. Смысл редукции заключается в уменьшении (часто весьма значительном) размерности пространства наблюдений.

Практический способ нахождения Д. с. основан на следующей теореме факторизации. Пусть семейство {Р_q} доминировано s-конечной мерой mи пусть р _q=dP_q/dm- плотность распределения Р _q относительно меры m. Статистика Xдостаточна для семейства {Р_q} в том и только в том случае, когда

где g_q , h- неотрицательные измеримые функции (hне зависит от q). Для дискретных распределений в качестве m можно взять "считающую" меру: в этом случае р _q.(w) в соотношении (*) имеет смысл вероятности элементарного события {w}.

Пусть, напр., X₁,..., Х _п- последовательность независимых случайных ведичин, принимающих значение 1 с неизвестной вероятностью v и значение О с вероятностью 1-v (схема Бернулли). Тогда

Равенство (*) выполняется7 если положить

Таким образом, эмпирическая частота

является Д. с. для неизвестной вероятности v в схеме Бернулли.

Пусть Х ₁, ..., Х _п- последовательность независимых нормально распределенных величин с неизвестными средним значением m и дисперсией а ². Совместная плотность распределения X₁, ..., Х _п по мере Лебега дается выражением

зависящим от х ₁,..., х _п только через величины

Поэтому векторная статистика

является Д. с. для двумерного параметра q=(m,s²). Д. с. здесь будет и совокупность выборочного среднего

и выборочной дисперсии

поскольку величины

могут быть выражены через и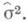

Для одного и того же семейства распределений может существовать много Д. с. В частности, тривиальной Д. с. является совокупность всех наблюдений [в рассмотренных выше примерах ( Х ₁, ..., Х _п)]. Однако основной интерес представляют статистики, позволяющие осуществить действительную редукцию статистич. задачи. Д. с. наз. минимальной, или необходимой, если она есть функция от любой другой Д. с. Необходимая Д. с. осуществляет максимально возможную редукцию статистич. задачи. В рассмотренных примерах найденные Д. с. являются необходимыми.

Важное применение понятия достаточности - метод улучшения несмещенных оценок, основанный на теореме Рао - Блэкуэлла - Кол моторова: если X- Д. с. для семейства {P_q}, Х ₁- произвольная статистика, принимающая значения в векторном пространстве R^d, то для действительной непрерывной выпуклой функции gна R^d

где - условное математич. ожидание статистики Х ₁ относительно X(к-рое фактически не зависит от 0 в силу достаточности X). В качестве функции потерь gздесь часто берется положительно определенная квадратичная форма на R^d.

Статистика Xназ. полной, если равенство Е _qf(X)=0, влечет f(Х)=0 почти наверное относительно Р _q , Одно из следствий теоремы Рао - Блэкуэлла - Колмогорова утверждает, что если существует полная Д. с. X, то она является равномерно по 0 наилучшей несмещенной оценкой своего математич. ожидания е(q)=Е _q Х. Подобная ситуация имеет место в приведенных примерах. Так, эмпирическая частота является равномерно наилучшей несмещенной оценкой вероятности v в схеме Бернулли, а выборочные среднее m и дисперсия m² - равномерно наилучшие несмещенные оценки параметров нормального распределения m и о ².

В теоретическом плане иногда удобнее иметь дело не с Д. с, а с достаточными сг-алгебрами. Если {Р _q; } - семейство распределений на вероятностном пространстве (W, A), то s-подалгебра наз. достаточной для {Р _q}, если для любого события существует вариант условной вероятности , не зависящий от 0. Статистика Xдостаточна тогда и только тогда, когда достаточна порождаемая ею s-подалгебра

Лит.:[1] Halmos P. R., Savage L. I., "Ann. Math. Statistics", 1949, v. 20, p. 225-41; [2] Колмогоров А. Н., "Изв. АН СССР. Сер. матем.", 1950, т. 14, № 4, с. 303-26; [3] Рао С. Р., Линейные статистические методы и их применения, пер. с англ., М., 1968.

А. С. Холево.