Akademik

приближенные методы решения - методы получения аналитич. выражений (формул), либо численных значений, приближающих с той или иной степенью точности искомое частное решение дифференциального уравнения (д. у.) или системы для одного или нескольких значений аргумента. Важность приближенных методов решения д. у. обусловливается тем, что точные решения в виде аналитич. выражений получаются лишь для немногих типов д. у.

Одним из старейших методов приближенного решения обыкновенных д. у. является метод разложения в ряд Тейлора. Согласно этому методу решение уравнения 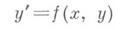с начальным условием

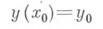
приближается отрезком ряда Тейлора

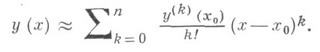
Производные y^(k)(x₀) выражаются через f(x, у )и ее частные производные:

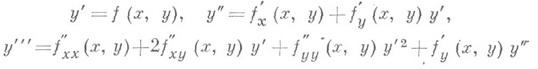
и т. д. Погрешность метода пропорциональна (х- х _о) ^п+1. При больших значениях х- х ₀ погрешность медленно стремится к нулю при а если значение х- х ₀ превосходит значение радиуса сходимости ряда Тейлора, то погрешность вообще не стремится к нулю при Это обстоятельство, а также необходимость, вычисления большого числа частных производных резко ограничивают область применения метода. Обычно метод разложения в ряд Тейлора, так же как и методы разложения в ряды более общего вида, применяют для нахождения приближенного решения в виде аналитич. выражения. К методам, применяемым для этой же цели, относятся Чаплыгина метод, использующий дифференциальные неравенства, и последовательных прибли жений метод. Эти методы применяются в основном в теоретич. исследованиях и редко используются для получения численных решений д. у. в практич. расчетаx.

В приложениях часто используются асимптотич. методы приближенного решения Д. у., основанные на выделении в решаемом уравнении главных членов и членов, малых по сравнению с главными. Примером может служить малого параметра метод для уравнения y'=f(x, у;m). Асимптотич. методы используются как для получения аналитич. выражении, приближающих решение, так и для исследований качественного поведения решений.

Наиболее распространенными методами численного решения д. у. являются методы, в к-рых решение ищется в виде таблицы приближенных значений искомой функции у(х)для ряда значений аргумента хиз отрезка 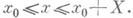Напр., пусть ищется решение уравнения у =f(x, у )с начальным условием у( х ₀) = у ₀ на отрезке в предположении, что решение вычисляется для значений аргумента

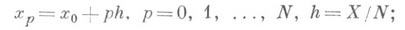
значения х _р наз. узлами, а величина h- шагом; через у _р обозначено значение приближенного решения в узле х _р.

Один из простейших численных методов - Эйлера метод основан на приближенном вычислении в тождестве

квадратуру по формуле прямоугольников:

Погрешность метода Эйлера пропорциональна h². Приближая интеграл

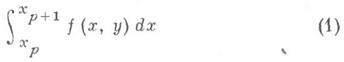
более точными квадратурными формулами, можно получить более точные численные методы. Напр., если воспользоваться для приближения (1) формулой трапеций, то

Обычно это уравнение неразрешимо относительно у _р+1. Для его решения можно воспользоваться итерационными методами, взяв в качестве начального приближения значение у _р+1, полученное по методу Эйлера. Одна итерация приводит к следующим формулам:

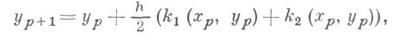
где

и

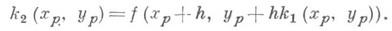
Эти формулы имеют погрешность порядка А ³. Они относятся к семейству Рунге- Кутта методов. Один из наиболее распространенных методов этого семейства имеет порядок погрешности А ⁵. Методы Рунге - Кутта наз. одношаговыми, так как для вычисления у _р+1 достаточно знать лишь у _р- значения приближенного решения на предыдущем шаге. Это обстоятельство позволяет применять формулы метода Рунге - Кутта для неравноотстоящих узлов, то есть в случае, когда разность х _р+1- х _р непостоянна. При выборе шага интегрирования полезно иметь в распоряжении нек-рую характеристику погрешности метода на шаге. Для оценки погрешности на шаге часто используется прием, называемый экстраполяцией по Ричардсону: y _р+2 вычисляется дважды - при помощи двух шагов hи одного шага 2h;полученные значения обозначаются через и 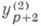соответственно; погрешность на шаге

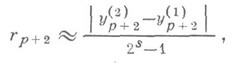
где s+1 - порядок r_p+2 пo h(для метода Эйлера s=l, для формулы трапеций s=2 и т. д.). Другой способ оценки погрешности на шаге состоит в получении формул метода Рунге - Кутта с контрольным членом, к-рый с точностью до малых более высокого порядка приближает главный член погрешности метода на шаге. Разработаны так наз. неявные одношаговые методы, к-рые оказались весьма эффективными для нек-рых классов задач.

Помимо семейства одношаговых методов для численного решения д. у. используются также и многошаговые методы (или конечноразностные). В этих методах для определения y_p+1 требуются не только у _р, но и значения y_p-i в нек-рых нескольких предыдущих узлах. Формулы k-шаговых методов имеют вид:

где a_-i, b_-i,- - постоянные, Если b₀=0, соответствующий метод наз. экстраполяционным, или явным; если b₀ неравно 0,- интерполяционным, или неявным, методом. Частным случаем мдогошаговых методов являются методы типа Адамса (см. Адамса метод):

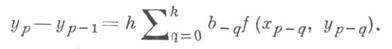
Обычно вычисления ведут по паре k-шаговых формул, одна из к-рых явная, а другая неявная. Такие пары формул наз. методами прогноза и коррекции. B качестве примера формул прогноза и коррекции можно привести формулы Хемминга:

имеющие на шаге погрешность порядка h⁶. При счете по формулам Хемминга сначала вычисляется "прогноз" затем - "поправка" затем - "коррекция" и, наконец,- приближенное решение y _р+1.

В небесной механике широко используются формулы Штермера (см. Штермера метод), особенно удобные для уравнений вида они имеют вид:

(явная формула Штермера) и

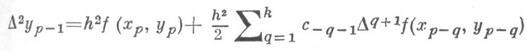
(неявная формула Штермера). В формулах Штермера

D^q(f)- конечная разность порядка q.

Применение многошаговых методов возможно лишь в случае, если известны значения решения в кпервых узлах. Для нахождения этих значений обычно пользуются одношаговыми методами, погрешность к-рых пропорциональна соответствующей степени h.

Иногда для вычисления y_p-q используется несколько предшествующих значений y_p-q, как в многошаговых методах, но в то же время на каждом шаге производится несколько вычислений правой части, как в методах Рунге - Кутта.

Решение краевых задач для обыкновенных д. у. обычно сводится к решению нескольких задач с начальными условиями. Простейшим методом такого рода является стрельбы метод, применяемый как к линейным, так и к нелинейным краевым задачам. Пусть, напр., требуется решить краевую задачу для одного уравнения 2-го порядка:

Полагая у'(0)=с, можно решить задачу с начальным условием

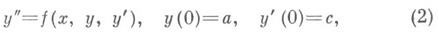
на отрезке и вычислить значение у(1, с). Из условия у(l, с ₀)=b определяется с ₀. Тогда решение краевой задачи будет совпадать с решением задачи с начальными условиями y(0)=а, у'(0)=с ₀. Корень с ₀ уравнения у(l, с)=b обычно ищется каким-либо приближенным методом и его нахождение связано с многократным решением задачи с начальными условиями (2). Метод стрельбы часто неустойчив к вычислительной погрешности.

Для линейных краевых задач часто применяют прогонки метод, при к-ром решение краевой задачи для уравнения 2-го порядка сводится к решению трех задач с начальным условием для уравнений 1-го порядка. Напр., пусть, решается краевая задача

Подбираются функции а(х)и b(х). такие, что у' (х)=а(х)у(х)+b (х)при всех Эти функции могут

быть получены как решения задач с начальными условиями

и

Решение этих задач наз. прямой прогонкой. В результате прямой прогонки получаются два условия для определения у(1). и у'(I):

Из этих условий находится y(l)-yi, после чего решение у(к)исходной краевой задачи получается как решение задачи с начальным условием

на отрезке - так наз. обратная прогонка. Методы стрельбы и прогонки применимы для решения краевых задач в случае систем д. у. В вычислительной практике широко используются разностные аналоги этих методов.

Для решения нелинейных краевых задач, кромо метода стрельбы, используют методы линеаризации в сочетании с методом прогонки. Наиболее распространенным методом этого класса является Ньютона метод.

При решении краевых задач применяются также и различные вариационные методы: Ритца метод, Галеркина метод и др. Вариационные методы сводят решение краевых задач к минимизации нек-рого функционала; приближение к решению ищется в задаваемом виде

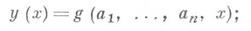
параметры а ₁, . . ., а _п определяются из условия минимума функционала.

Большинство численных методов решения обыкновенных д. у. реализовано в виде библиотечных программ ЭВМ.

Кроме аналитических и численных методов для приближенного решения обыкновенных д. у. применяются графич. методы, напр, метод изоклин, связанный с построением поля направлений, определяемого д. у. Применяются также аналоговые вычислительные машины и другие моделирующие устройства.

Лит.:[1] Бахвалов Н. С, Численные методы, М., 1973; [2] Березин И. С, Жидков Н. П., Методы вычислений, т. 2, 2 изд., М., 1962; [3]Михлин С. Г., Смолицкий X. Л., Приближенные методы решения дифференциальных и интегральных уравнений, М., 1965; [4] Моисеев Н. Н., Численные методы в теории оптимальных систем, М., 1971; [5} Милн В. Э., Численное решение дифференциальных уравнений, пер. с англ., М., 1955; [6] Коллатц Л., Численные методы решения дифференциальных уравнении, пер. с нем., М., 1953; [7] Xемминг Р. В., Численные методы..., пер. с англ., 2 изд., М., 1972; [8] Годунов С. К., Рябенький В. С, Разностные схемы. Введение в теорию, М., 1973; [9] Коллатц Л., Задачи на собственные значения..., пер. с нем., М., 1968.

С. С. Гайсарян.