Akademik

- общее название ряда теорем, позволяющих устанавливать доказуемость импликации в случае, когда дан логический вывод формулы Виз формулы А. В простейшем случае классического, интуиционистского и т. п. исчислений высказываний Д. т. утверждает: если Г, (из допущений Г, Авыводимо В), то

(*)

(Г может быть пусто). При наличии кванторов аналогичное утверждение неверно:

но не

Одна из формулировок Д. т. для традиционных исчислений предикатов (классического, интуиционистского и т. п.): если Г, А|-В, то

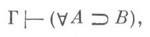
где означает результат приписывания V -кванторов (см. Квантор )по всем свободным переменным формулы А. В частности, если А- замкнутая формула, Д. т. принимает форму (*). Эта формулировка Д. т. дает возможность сводить поиск вывода в аксиоматич. теориях к поиску вывода в исчислении предикатов: формула В выводима из аксиом A₁, ...,A_n тогда и

только тогда, когда в исчислении предикатов выводима формула

Похожим образом формулируется Д. т. для логик, где имеются связки, "похожие" на кванторы. Так, для модальных логик S4 и S5 Д. т. имеет вид: если Г,то

Более тонкие формулы Д. т. получаются, если вводить V-кванторы не по всем свободным переменным, а лишь по тем, к-рые связываются кванторами в процессе вывода. Говорят, что переменная y варьируется для формулы А в данном выводе, если увходит свободно в Аи в рассматриваемом выводе имеется применение правила введения V в заключение импликации (или введения Э в посылку), при к-ром вводится квантор по y, причем посылка этого применения зависит в данном выводе от А. Теперь Д. т. для традиционных исчислений предикатов уточняется так: если Г, то

где y₁, ... , у _п- полный список переменных, к-рые варьируются для Ав данном выводе. В частности, если никакая свободная переменная из Ане варьируется, то Д. т. принимает форму (*). При формулировке соответствующего уточнения Д. т. для модальных логик следует считать, что варьирование происходит в правилах введения в заключение импликации и - в посылку.

При установлении Д. т. для исчислений релевантной импликации (т. е. для систем, согласованных с истолкованием как Ввыводимо с существенным использованием допущения А)приходится либо модифицировать само понятие вывода, либо считать, что варьирование происходит при всяком использовании "постороннего" допущения; напр., при переходе от пары А, к А,варьируется формула А, т. к. она не входит во второй член. пары.

Если Ане варьируется в данном выводе, то Д. т. принимает форму (*), а если Аварьируется, то Д. т. принимает вид: если А, Г|- В , то

где t- константа "истина" (или конъюнкция формул () для всех пропозициональных переменных р, выходящих в Л, Г, В).

Лит.:[1] Клини С. К., Введение в метаматематику, пер. с англ., М., 1957; [2] Карри X. Б., Основания математической логики, пер. с англ., М., 1969.

Г. Е. Минц.