сложное (или ангармоническое) отношение, четырех точек М 1, М 2, М 3, M4 на прямой - число, обозначаемое символом ( М 1 М 2 М 3 М 4 )и равное
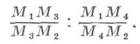
При этом отношение M1M3/M3M2 считается положительным, если направления отрезков М 1 М 3 и М 3 М 2 совпадают, и - отрицательным при различных направлениях. Д. о. зависит от порядка нумерации точек, к-рый может отличаться от порядка следования точек на прямой. Наряду с Д. о. четырех точек, рассматривается Д. о. четырех прямых т 1, т 2, т 3, m4, проходящих через точку. Это отношение обозначается символом ( т 1 т 2 т 3 т 4). Оно равно
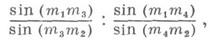
причем угол (mimj )между прямыми mi и т j рассматривается со знаком. .
Если точки М 1, М 2, М 3, М 4 лежат на прямых m1 т 2, т 3, т 4, то
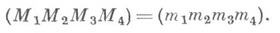
Если точки M1, M2, М 3, М 4 и M1', M2', М 3', М 4' получены пересечением одной четверки прямых т 1, т 2, т 3, m4, то ( М 1 М 2 М 3 М 4)=( М 1'М 2'М 3'М 4').
Д. о. является инвариантом проективных преобразований. Д. о., равное -1, наз. гармоническим отношением (см. Гармоническая четверка точек).
Э. Г. Позняк.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.